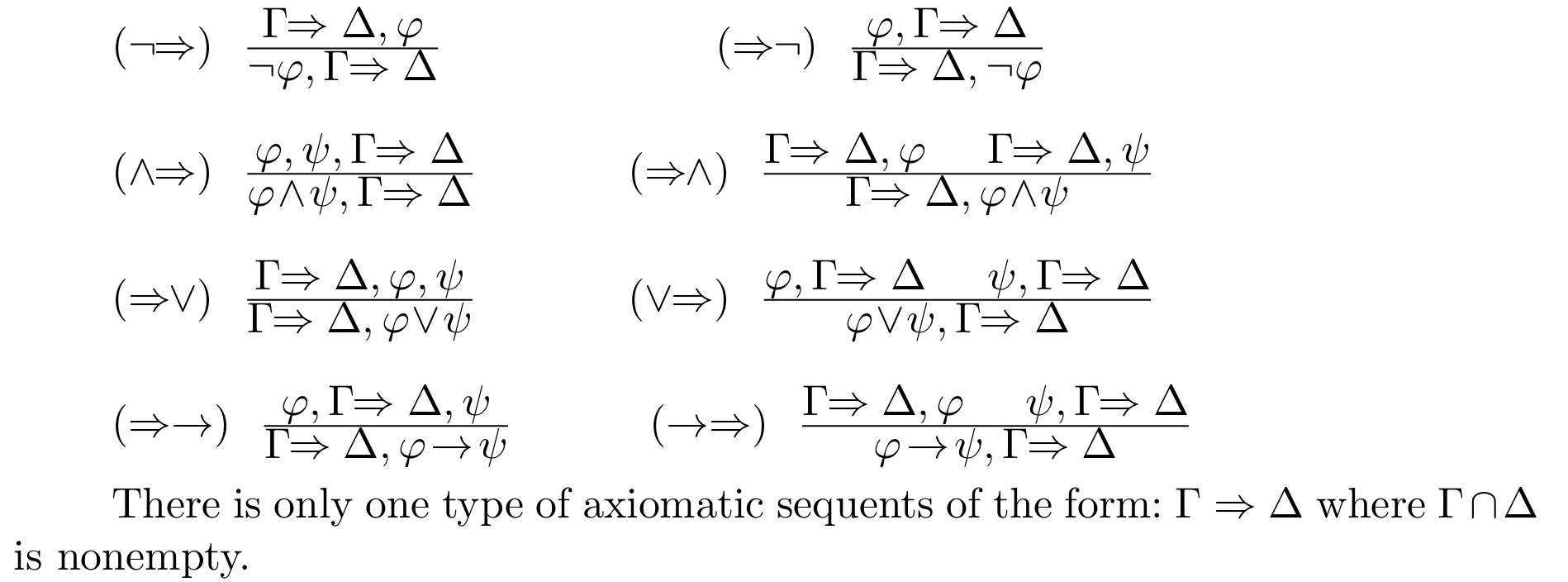简单集合论

Cantor-Bernstein 定理：两集合互有单射，则必有双射

对于集合 S,TS,T ，如果存在单射 f:S→Tf:S\rightarrow T 和 g:T→Sg:T\rightarrow S ，则 S,TS,T 之间存在双射。

证明：可以构造一个二分图，左部是 SS ，右部是 TT ，那么图是由环和链构成，其中链没有终点，只有起点。

于是对于从 TT 开始的链，可以令 φ(x)=g−1(x)\varphi(x)=g^{-1}(x) ，否则令 φ(x)=f(x)\varphi(x)=f(x) 。

环的话就令 φ(x)=f(x)\varphi(x)=f(x) 即可。

Cantor 定理： 不存在 2S2^S 到 SS 的单射。

假设 φ:2S→S\varphi:2^S\rightarrow S 是单射。

令 A=φ(2S)A=\varphi(2^S) ，T={x∈A∣x∉φ−1(x)}T=\{x\in A|x\notin \varphi^{-1}(x)\} 。

那么 T∈2ST\in 2^S 。令 a=φ(T)a=\varphi(T)

如果 a∈Ta\in T ，则 a∉φ−1(a)=Ta\notin \varphi^{-1}(a)=T ，矛盾

如果 a∉Ta\notin T ，则 a∈A−Ta\in A-T ，那么 a∈φ−1(a)=Ta\in \varphi^{-1}(a)=T ，矛盾

综上，不存在这样的 φ\varphi 。

结论：R∼2NR\sim 2^N

先找 2N→R2^N\rightarrow R 的单射：令 φ(S)=∑x∈S3−x\varphi(S)=\sum\limits_{x\in S}3^{-x} 即可。

再找 R→2NR\rightarrow 2^N 的单射，我们分为两步。

先找 R→(0,1)R\rightarrow (0,1) ，其实有 R∼(0,1)R\sim (0,1) ，构造 f:(0,1)→Rf:(0,1)\rightarrow R 满足 f(x)=tan⁡(π2(2x−1))f(x)=\tan(\frac{\pi}{2}(2x-1)) ，这是双射。

再找 (0,1)→2N(0,1)\rightarrow 2^N ，考虑把一个 (0,1)(0,1) 间的数看成是二进制小数，问题在于它有两种表示方式：无限 00 结尾，无限 11 结尾，限制为前者即可。

结论：N∼QN\sim Q

N→QN\rightarrow Q 显然。

Q→Z×NQ\rightarrow Z×N ：把一个有理数写成整数除以正整数的形式。

Z×N→NZ×N\rightarrow N ： 我们只需要把这些数对按照一个顺序排列，依次编号。可以蛇形地进行编号，虽然最后的形式比较丑，但确实很对。

基数乘幂规则：(ST)W∼ST×W(S^T)^W\sim S^{T×W}

考虑 h:W→STh:W\rightarrow S^T 。现在构造 φ(h):T×W→S\varphi(h):T×W\rightarrow S 。考虑 φ(h)(x,y)=h(y)(x)\varphi(h)(x,y)=h(y)(x) 即可。这个显然是双射。

结论：A∼A′,B∼B′→AB∼A′B′A\sim A',B\sim B'\rightarrow A^B\sim A'^{B'}

对于 h:B→Ah:B\rightarrow A ，构造 φ(h):B′→A′\varphi(h):B'\rightarrow A' 满足 φ(h)(b′)=(h(b))′\varphi(h)(b')=(h(b))'

结论：RN∼RR^N\sim R

R→RNR\rightarrow R^N 显然：对于 x∈Rx\in R ，构造 f:N→Rf:N\rightarrow R 满足 f(0)=x,f(1)=0,f(2)=0,…f(0)=x,f(1)=0,f(2)=0,\dots ，然后令 φ(x)=f\varphi(x)=f 。

RN→RR^N\rightarrow R ：对于 f∈RNf\in R^N ，我们可以蛇形串起来 f(0),f(1),f(2),…f(0),f(1),f(2),\dots ，得到一个实数…。哎，这个构造很魔怔。

另一个证法： RN∼(2N)N∼2N×N∼2N∼RR^N\sim (2^N)^N\sim 2^{N×N}\sim 2^N\sim R 。

偏序

a≤a,a≤b∧b≤c→a≤c,a≤b∧b≤a→a=ba\le a,a\le b\land b\le c\rightarrow a\le c,a\le b\land b\le a\rightarrow a=b

全序：偏序基础上，任意二者都可比较，也就是 a≤b∨b≤aa\le b\lor b\le a

良序：全序基础上，∀S,∃a∈S,∀b∈S,a≤b\forall S,\exists a\in S,\forall b\in S,a\le b

良序定理

任意集合都能找到一个序，这个序是良序的

连续统假设（CH）

是否有一个集合的势在 ∣N∣|N| 和 ∣R∣|R| 之间？前人已经证明：在现有的数学体系下，无法证明这件事是否成立。是，或不是，可以引出两套独立的理论。

命题逻辑

一些符号

原子命题（Atomic Propositions）：P,Q,P1,P2,⊥,⊤,…P,Q,P_1,P_2,\bot,\top,\dots

逻辑联结词 (Logical Connectives)：∨,∧,  ⟹  ,  ⟺  ,¬\lor,\land,\implies,\iff,\lnot …

辅助符号 (Auxiliary Symbols)：()()…

我们把这个字母表记作 Σ\Sigma 。

Σ∗=⋃i=0+∞Σi\Sigma^{*}=\bigcup\limits_{i=0}^{+\infty}\Sigma^i ，表示所有有限字符串的集合。

接下来定义下面的 X⊆Σ∗X\subseteq \Sigma^{*} 合法：

  1. 单独的原子命题都在 XX 中。

  2. 如果 P,Q∈XP,Q\in X ，则 (P∧Q),(P∨Q),(P  ⟺  Q),(P  ⟹  Q),⋯∈X(P\land Q),(P\lor Q),(P\iff Q),(P\implies Q),\dots\in X

  3. 如果 P∈XP\in X ，则 (¬P)∈X(\lnot P)\in X

满足上面条件的最小的 XX 被称为 PROP。

比如说 (P→Q)∈PROP(P\rightarrow Q)\in PROP ，而 P→Q∉PROPP\rightarrow Q\notin PROP ，但实际上对一个命题我们都默认去掉最外层括号

我们称一个 v:PROP→{0,1}v:PROP\rightarrow \{0,1\} 是赋值，定义原子命题的真值表即可

重言式 (tautology) ：对任意赋值 vv ，都有 [φ]v=1[\varphi]_v=1 。可以记作 ⊨φ\models\varphi

Γ⊨ψ\Gamma\models \psi ：对于任意赋值 vv ，如果 ∀φ∈Γ,[φ]v=1\forall \varphi\in \Gamma,[\varphi]_v=1 ，则 [ψ]v=1[\psi]_v=1

φ⊨ψ\varphi\models \psi ：对于任意赋值 vv ，有 [φ]v≤[ψ]v[\varphi]_v\le [\psi]_v

自然演绎（Natural Deduction）

自然演绎系统推导规则：

φφ→ψψ\frac{\varphi\quad \varphi \rightarrow \psi}{\psi} ，这被称为假言消去，符号是 →E\rightarrow E

φψφ∧ψ\frac{\varphi\quad \psi}{\varphi\land \psi} ，这被称为合取引入，符号是 ∧I\land I

φ∧ψφ\frac{\varphi \land \psi}{\varphi} ，这被称为合取消去，符号是 ∧E\land E

[¬φ]⊥φ\frac{\frac{[\lnot \varphi]}{\bot}}{\varphi} ，这是矛盾引入，符号是 RAA

[φ]ψφ→ψ\frac{\frac{[\varphi]}{\psi}}{\varphi\rightarrow \psi} ，这是蕴含引入，符号是 →I\rightarrow I

⊥φ\frac{\bot}{\varphi} ，这是爆炸原理

自然演绎具有完备性，也就是说 PROP 里每一条重言式，都能被自然演绎系统证明。

我们来做一个往年期中题。r→p⊢((p→q)→r)→pr\rightarrow p\vdash ((p\rightarrow q)\rightarrow r)\rightarrow p

  1. r→pr\rightarrow p (known)

  2. [(p→q)→r][(p\rightarrow q)\rightarrow r]

  3. [¬p][\lnot p]

  4. [p][p]

  5. ⊥(3,4,¬E)\bot(3,4,\lnot E)

  6. q(5,⊥φ)q(5,\frac{\bot}{\varphi})

  7. p→q(5,6,→I)p\rightarrow q(5,6,\rightarrow I)

  8. r(2,7,→E)r(2,7,\rightarrow E)

  9. p(1,8,→E)p(1,8,\rightarrow E)

  10. ⊥(3,9,¬E)\bot(3,9,\lnot E)

  11. p(3,10,RAA)p(3,10,RAA)

  12. ((p→q)→r)→p(2,11,→I)((p\rightarrow q)\rightarrow r)\rightarrow p(2,11,\rightarrow I)

大概讲一下我的思考过程，首先 [(p→q)→r][(p\rightarrow q)\rightarrow r] 是显然的，只要接下来能导出 pp 就证完了。

那就反证，[¬p][\lnot p] ，有 ¬p⊢p→q\lnot p\vdash p\rightarrow q ，然而这个不是标准步骤，所以得拆开了写。

然后就能通过 [(p→q)→r][(p\rightarrow q)\rightarrow r] 和 p→qp\rightarrow q 得到 rr 了。

又有 r→pr\rightarrow p ，导出 pp ，这和假设矛盾！于是有 pp ，证明结束。

还有另一个往年期中题：(p→q)→(¬q→¬p)(p\rightarrow q)\rightarrow (\lnot q\rightarrow \lnot p) 和 (¬q→¬p)→(p→q)(\lnot q\rightarrow \lnot p)\rightarrow (p\rightarrow q) ，其中哪个能用不带 RAA 的自然演绎证出来？

没有 RAA 其实被称为 直觉主义逻辑 ，它认为双重否定不是肯定。

我们其实还是能用反证法，但只能在 φ\varphi 的假设和 ⊥\bot 的基础上，利用 →I\rightarrow I 推出 ¬φ\lnot \varphi 。

此处只有前者能被证明，证明如下：

1.p→q2.[¬q]3.[p]4.q(2,3,→E)1.p\rightarrow q \quad 2.[\lnot q] \quad 3.[p] \quad 4.q(2,3,\rightarrow E)

5.⊥(2,4,¬E)6.¬p(3,5,→I),7.¬q→¬p(2,6,→I)5.\bot (2,4,\lnot E)\quad 6.\lnot p(3,5,\rightarrow I),7.\neg q\rightarrow \neg p(2,6,\rightarrow I)

System K

我们先说明一下 Γ⇒Δ\Gamma\Rightarrow \Delta 的含义：

对于任意赋值 vv 都有：如果 ∀φ∈Γ,[φ]v=1\forall \varphi \in \Gamma,[\varphi]_v=1 ，则 ∃ψ∈Δ,[ψ]v=1\exists \psi\in \Delta,[\psi]_v=1 。

然后有以下八个定理：

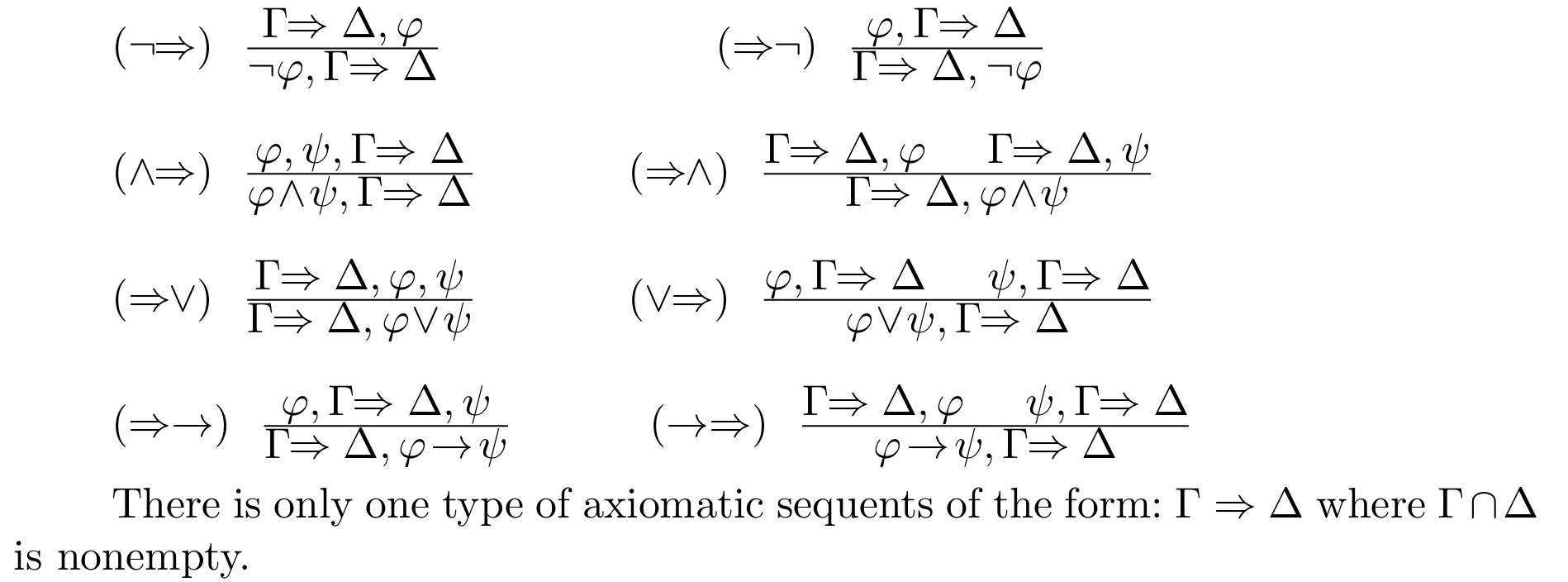
2025-09-16-17-37-02-f0e5c9b8-1f8a-4dac-a381-1935bae671d6

自然演绎的一致性，完备性

Γ⊨φ\Gamma\models \varphi

对任意赋值 vv ，如果 ∀ψ∈Γ,[ψ]v=1\forall \psi\in \Gamma,[\psi]_v=1 ，则 [φ]v=1[\varphi]_v=1

Γ⊢φ\Gamma\vdash\varphi

对任意赋值 vv ，如果 ∀ψ∈Γ,[ψ]v=1\forall \psi\in \Gamma,[\psi]_v=1 ，则可以证明 [φ]v=1[\varphi]_v=1 。

一致性 (Soundness)

如果 Γ⊢φ\Gamma\vdash\varphi 则 Γ⊨φ\Gamma\models \varphi

也就是说一个系统所有的规则都是对的。

完备性(Completeness)

如果 Γ⊨φ\Gamma\models \varphi 则 Γ⊢φ\Gamma\vdash\varphi 。

也就是说啥都能证。

接下来证明自然演绎的完备性。

引理： Γ,ψ⊢φ\Gamma,\psi\vdash \varphi 且 Γ,¬ψ⊢φ\Gamma,\lnot\psi\vdash \varphi ，就能有 Γ⊢φ\Gamma\vdash \varphi

那现在想证明 Γ⊢φ\Gamma\vdash\varphi ，如果有一个原子命题 P1P_1 分别满足 Γ,P1⊢φ\Gamma,P_1\vdash \varphi 和 Γ,¬P1⊢φ\Gamma,\lnot P_1\vdash \varphi ，那就结束了。

类似的，我们递归的添加 P2,P3P_2,P_3 ，直至添加所有原子命题。

对于一个赋值 vv ，令其对应的集合 VV 是： [Pi]v=1[P_i]_v=1 则把 PiP_i 加入 VV ，否则把 ¬Pi\lnot P_i加入 VV 。

我们只要能证明对任意赋值 vv ，都有 Γ,V⊢φ\Gamma,V\vdash \varphi ，那就结束了。

引理：

对于一个赋值 vv ，若 [φ]v=1[\varphi]_v=1 则 V⊢φV\vdash \varphi ，否则 V⊢¬φV\vdash \lnot \varphi

引理证明：需要归纳。

φ\varphi 是原子命题则显然成立。

φ=φ1→φ2\varphi=\varphi_1\rightarrow \varphi_2 ：分类讨论即可。

举个例子，就是说 V⊢φ1,V⊢¬φ2V\vdash \varphi_1,V\vdash \lnot\varphi_2 之后能否证明 V⊢¬φV\vdash \lnot \varphi 。

是可以的， [φ1→φ2][\varphi_1\rightarrow \varphi_2] ，导出 φ2\varphi_2 ，和 ¬φ2\lnot \varphi_2 形成 ⊥\bot ，于是就有 ¬φ\lnot \varphi 了。

其他连接词类似，都用自然演绎来证。

证完引理之后，因为 Γ⊨φ\Gamma\models \varphi 在前，本来就有 [φ]v=1[\varphi]_v=1 ，或者存在 ψ∈Γ\psi\in \Gamma 使得 [¬ψ]v=1[\lnot\psi]_v=1 。

[φ]v=1[\varphi]_v=1 的话，直接就有 V⊢φV\vdash \varphi 了。

存在 [ψ]v=0[\psi]_v=0 的话，就可以导出 ⊥\bot ，从而得到 φ\varphi 。也就是说 Γ,V⊢⊥⊢φ\Gamma,V\vdash\bot\vdash \varphi

Predictate Logic（一阶逻辑，谓词逻辑）

字母表：

  1. 常元 a,b,c,c1,c2,…a,b,c,c_1,c_2,\dots

  2. 变量 x,y,z,x1,x2,x3,…x,y,z,x_1,x_2,x_3,\dots

  3. 函数 f,g,h,f1,f2,f3,…f,g,h,f_1,f_2,f_3,\dots

  4. 谓词 P,Q,P1,P2,…P,Q,P_1,P_2,\dots

  5. 连接词 ∧,→\land,\to 等

  6. 辅助词 () 等

  7. 量词 ∀,∃\forall ,\exists

定义 TERM：

∀\forall 变量 xx ，x∈Xx\in X

∀t1,t2,⋯∈X\forall t_1,t_2,\dots\in X 和函数 ff ，f(t1,t2,… )∈Xf(t_1,t_2,\dots)\in X

TERM\text{TERM} 是满足上述条件的最小的 XX。

定义 FOR(formula)：

对于任意谓词 PP 和 terms t1,t2,…t_1,t_2,\dots P(t1t2)∈XP(t_1\quad t_2)\in X

∀φ,ψ∈X\forall \varphi,\psi\in X ，φ→ψ,φ∧ψ⋯∈X\varphi\to \psi,\varphi\land \psi\dots\in X

∀φ∈X\forall \varphi\in X 和变量 xx ，

∀xφ∈X,∃xφ∈X\forall x\quad \varphi \in X,\exists x\quad \varphi\in X

FOR\text{FOR} 是满足上述条件的最小 XX

定义 Structure：

包含论域 Ω\Omega ，函数 Ωn→Ω\Omega^n\rightarrow \Omega ，谓词 P:Ωn→{0,1}P:\Omega^n\rightarrow \{0,1\} ，还有常元的对应值。

我的理解：在一个 structure 中，常元和函数的规则就确定了每个 term 在变量赋值后对应 universe 中哪个值。

而 predicate 的规则决定了每个原子公式的 true or false。当然这里也是在 term 中的变量赋值后得到的。

符号记作 𝔄𝔄 。可以把 𝔄𝔄 看做命题逻辑里的 valuation。

对于 𝔄𝔄 的一个函数 ff ，记它对应的那个原本的函数是 f‾\overline{f} ，那么 [f‾(t1,t2)]𝔄=f([t1]𝔄,[t2]𝔄)[\overline{f}(t_1,t_2)]_{𝔄}=f([t_1]_𝔄,[t_2]_{𝔄})

其他也是类似。

φ[t/x]\varphi[t/x] ：将 φ\varphi 中 xx 的所有自由出现替换为 tt 。前提条件：安全性，即替换成 tt 之后，tt 不会因为前面的量词变成 bounded var。

设 FV(φ)FV(\varphi) 是 φ\varphi 中的自由变量集合，V(φ)V(\varphi) 是变量集合。

𝔄⊨φ𝔄\models \varphi 的定义：

若 FV(φ)=∅FV(\varphi)=\empty ，则 𝔄⊨φ𝔄\models \varphi 等同于 [φ]𝔄=1[\varphi]_{𝔄}=1

否则，我们认为是 ∀x1∀x2…φ\forall x_1\forall x_2\dots \varphi ，其中 x1,x2,…x_1,x_2,\dots 表示所有 FV(φ)FV(\varphi) 中的元素

𝔄⊨Γ𝔄\models \Gamma 等价于 ∀φ∈Γ,𝔄⊨φ\forall \varphi\in \Gamma,𝔄\models \varphi

Γ⊨φ\Gamma\models \varphi ：如果 𝔄⊨Γ𝔄\models \Gamma ,则 𝔄⊨φ𝔄\models \varphi 。

一阶逻辑中的自然演绎和等号公理

φ(x)∀xφ(x)(∀I)\frac{\varphi(x)}{\forall x\varphi(x)}(\forall I)

∀xφ(x)φ(t)(∀E)\frac{\forall x \varphi(x)}{\varphi(t)}(\forall E)

我们认为 ∃\exists 就是 ¬∀¬\lnot \forall \lnot ，可以想想 ∀xφ(x)⊢∃xφ(x)\forall x\varphi(x)\vdash \exists x \varphi(x) 是怎么做的。

等号公理：

x=xx=x

x=y→y=xx=y\to y=x

(x=y)∧(y=z)→x=z(x=y)\land (y=z)\to x=z

(x1=y1)∧(x2=y2)∧⋯→t(x1,x2,… )=t(y1,y2,… )(x_1=y_1)\land(x_2=y_2)\land\dots \to t(x_1,x_2,\dots)=t(y_1,y_2,\dots)

皮亚诺公理（Peano Axiom）

这是一套用来定义自然数的公理，它包含函数 +,⋅,S+,\cdot,S 和零元 00 ，单位元 11 ，其中可以认为 S(x)S(x) 是 xx 的后继

∀x¬(S(x)=0)\forall x \lnot (S(x)=0)

∀x∀y(S(x)=S(y))→(x=y)\forall x\forall y\quad(S(x)=S(y))\to (x=y)

∀xx+0=x\forall x \quad x+0=x

∀x∀yx+S(y)=S(x+y)\forall x\forall y\quad x+S(y)=S(x+y)

∀xx⋅1=x\forall x\quad x\cdot 1=x

∀x∀yx⋅S(y)=x⋅y+x\forall x\forall y\quad x\cdot S(y)=x\cdot y+x

φ(0)∧∀xφ(x)→φ(S(x))\varphi(0)\land \forall x \quad\varphi(x)\to \varphi(S(x)) ，则 ∀xφ(x)\forall x\quad\varphi(x)

皮亚诺公理加上一阶逻辑本身的公理，就可以在自然数上做一些证明了。比如说证 ∀x0+x=x\forall x\quad 0+x=x,可以想一想

一阶理论(theory) 一个由公理和所有能从公理推导出的定理组成的集合 TT。如果 T⊢φT\vdash \varphi ，则 φ∈T\varphi\in T 。

亨金性质 一个理论 T 是 henkin theory ，当且仅当所有 TT 中形如 ∃xφ(x)\exists x \varphi(x) 的句子，都存在常量 cc 使得 φ(c)∈T\varphi(c)\in T 。

定义理论的扩张：

如果 T2T_2 是 T1T_1 的扩张，则 T2T_2 使用的语言 (即它的符号，如常量、函数、谓词) 必须包含 T1T_1 的所有语言。在 T1T_1 中可证的公式，在 T2T_2 也是可证的。

保守扩张(conservative extension)

就是说 T2T_2 是 T1T_1 的扩张，且 T2T_2 中所有能被 T1T_1 的语言写出的能证明的公式，在 T1T_1 也能被证明。

亨金扩张

对于一个给定的理论 TT，它的亨金扩张 THT_H​ 是通过一个系统性的过程构造出来的。这个过程会：

  1. 对所有形如 ∃xφ(x)∃x\varphi(x) 的句子，引入一个新的常量符号 cφc_\varphi​。这个 cc 被称为亨金常量。

  2. 为每个新引入的常量 cφc_\varphi，增加一条新的公理：∃xφ(x)→φ(cφ)∃xφ(x)→φ(c_\varphi)

我们记这样的单步扩张为 T∗T^* ，可以证明 T∗T^* 是保守扩张。然后不断这样扩张下去，最终得到的理论就是 TT 的亨金扩张 THT_H​，THT_H 显然是 henkin theory。

接下来对 THT_H 再做一次扩展：枚举 THT_H 的语言能写出的所有命题 φ\varphi ，如果 φ,¬φ∉TH\varphi,\lnot\varphi\notin T_H ，则 TH,φT_H,\varphi 一定不会导出 bot，所以把 φ,¬φ\varphi,\lnot\varphi 二者任取一加入 THT_H ，得到一个新的理论 TMCT_{MC} 。

接下来可以构造一个 model MM 。

注意这里我们定义了 model ，它是一个特殊的 structure ，如果 MM 是 TT 的 Models，则 ∀φ∈T\forall \varphi\in T ，φM=1\varphi^M=1 。其实在命题逻辑里也有一个定义完全一样的相对于 valuation 的 model，但我们之前没提到。

对于 TMCT_{MC} ，我们首先定义 closed terms，它是指无变量的 terms 。

我们可以在 closed terms 之间定义一个等价关系，即 a∼b↔a=b∈TMCa\sim b\leftrightarrow a=b\in T_{MC} 。基于等号公理，可以证明它确实是等价关系。

比如说对于一个包含了自然演绎和皮亚诺公理的理论，我们会认为 S(0)+S(0)S(0)+S(0) 和 S(S(0))S(S(0)) 在一个等价类，毕竟 1+1=21+1=2 （虽然证明不平凡）

然后我们认为 MM 的论域是这些等价类构成的集合。比如一个只包含自然演绎和皮亚诺公理的理论，它在这个定义下的论域其实就是自然数集合。

继续我们的定义，对于常量，cM=[c]c^M=[c] ，对于函数，fM([x1],[x2],…,[xm])=[f(x1,x2,…,xm)]f^M([x_1],[x_2],\dots,[x_m])=[f(x_1,x_2,\dots,x_m)] 。对于谓词，PM([x1],[x2],…,[xm])P^M([x_1],[x_2],\dots,[x_m]) 成立当且仅当 P(x1,x2,…,xm)∈TMCP(x_1,x_2,\dots,x_m)\in T_{MC}

那这个模型有啥用？ 由于 TMCT_{MC} 是 TT 的一系列保守扩张， 可以证明 MM 是 TT 的一个模型。

哥德尔完备性定理

经典一阶逻辑中的任意一个一致的理论都能找到一个模型。

然后它有一个等价的结论：T⊢φ↔T⊨φT\vdash \varphi\leftrightarrow T\models \varphi ，其中 T⊨φT\models \varphi 代表它的任意模型 MM 有 M⊨φM\models \varphi 。

（说实话，我这里肯定是没完全搞懂证明过程的，只是大致记录了老师和 gemini 在说什么，可能也没记录对）

集合论

Axiom of Extensionality (外延性公理)

∀x,y(∀δδ∈x↔δ∈y)\forall x,y(\forall \delta\quad\delta\in x\leftrightarrow\delta\in y) 则 x=yx=y

Axiom schema of specification （分离公理模式）

对任意谓词 φ\varphi

∀A∃B∀x(x∈B↔x∈A∧φ(x))\forall A\exists B\forall x(x\in B\leftrightarrow x\in A\land \varphi(x))

这是为了定义 yφ={δ∈x∣φ(δ)}y_\varphi=\{\delta\in x|\varphi(\delta)\}

当然这个谓词可能会加入更多 terms，原理是一样的

Axiom of pairing 配对公理

这是为了定义 δ={x,y}\delta=\{x,y\}

$\forall x,y\exists \delta $ 使得 x∈δx\in \delta 且 y∈δy\in\delta

Axiom of union 并集公理

这是为了定义 ∪\cup

∀x∃y∀w,δ(δ∈x∧w∈δ→w∈y)\forall x\exists y\forall w,\delta (\delta\in x\land w\in\delta\to w\in y)

Axiom of power set 幂集公理

这是为了定义 y=2xy=2^x

∀x∃y∀z(z⊆x→z∈y)\forall x\exists y \forall z(z\subseteq x \to z\in y)

Axiom of infinity 无穷公理

∃N(∅∈N∧(∀y,y∈N→y∪{y}∈N))\exists N (\empty\in N\land (\forall y,y\in N\to y\cup \{y\}\in N))

Axiom Schema of Replacement 替换公理模式

这是为了定义 B=fw(A)B=f_w(A)

对任意函数关系 φ(x,y)\varphi(x,y) ，有 ∀x∃y∀a(a∈y↔∃b∈x,φ(b,a))\forall x\exists y\forall a(a\in y\leftrightarrow \exists b\in x,\varphi(b,a))

Axiom of Regularity 正则公理

∀A(A≠∅→∃x(x∈A∧x∩A=∅))∀A(A\neq\empty\to \exists x(x\in A\land x\cap A=\empty))

Axiom of Choice 选择公理

∀S(∀xx∈S→x≠∅∧∀x,y(x∈S∧y∈S)→x∧y=∅)\forall S(\forall x\quad x\in S\to x\neq\empty\land\forall x,y(x\in S\land y\in S)\to x\land y=\empty)

则 ∃T∀xx∈S→∃yy∈S∩T\exists T \forall x\quad x\in S\to \exists y\quad y\in S\cap T

直观来说，就是说如果有若干个苹果袋子构成了一个集合，则保证你能构造一个袋子，它能在每个袋子中都取一个苹果。

（这里的苹果，袋子其实都是集合）

现在我们证明哥德尔不完备定理，也就是说：任何无矛盾的公理体系，只要包含初等算术的陈述，则必定存在一个不可判定命题，用这组公理不能判定其真假。

我们希望构造一个语句使得它的含义是：它本身不能被证明

简单来讲，首先对所有语句做一个 encoding，映射到一个自然数，这样就可以把 TERM,FORTERM,FOR 定义成一个自然数的集合。

自然我们又能定义 PROVPROV ，表示一个理论能证出来的自然数的集合。

对角线引理：对任意一个带一个自由变元的算术公式 ψ(x)\psi(x) ，都存在 φ\varphi 使得 PA⊢φ↔ψ(id(φ))PA\vdash \varphi\leftrightarrow \psi(id(\varphi))

所以令 ψ=¬PROV\psi=\lnot PROV ，即可找到一个语句 φ\varphi 使得 φ↔¬PROV(id(φ))\varphi\leftrightarrow\lnot PROV(id(\varphi)) 。这个 φ\varphi 就是我们想要的东西了。

最后可以证明 φ\varphi 和 ¬φ\lnot \varphi 都不可能在 PROVPROV 中，证明就结束了，细节我懒得管了。

初等数论

除数，被除数，余数：可以证明 ∀a>0∀b∃!q,r\forall a>0 \forall b\exists!q,r 使得 b=aq+rb=aq+r 且 r∈{0,1,…,q−1}r\in \{0,1,\dots,q-1\} ，这可以固定 aa ，对 bb 归纳证明。

Prime(n)\text{Prime}(n) 可以看做 (n≠1)∧(∀a∈Na∣n→(a=1∨a=n))(n\neq 1)\land(\forall a\in \N\quad a|n\to (a=1\lor a=n))

gcd⁡(a,b)\gcd(a,b) ：最大的正整数 kk 使得 k∣ak|a 且 k∣bk|b

特别的，gcd⁡(0,n)=n\gcd(0,n)=n

gcd′(a,b)gcd'(a,b) ：最小的 am+bn∈Z+am+bn\in \Z^+ ，其中 m,n∈Zm,n\in \Z 。

我们证明 gcd′(a,b)=gcd(a,b)gcd'(a,b)=gcd(a,b) ：考虑 exgcd 即可

质因数分解(Factorization)：n=p1p2…ptn=p_1p_2\dots p_t 可以证明分解是唯一的：

归纳证明，对于 nn 的两组分解 p1p2…ptp_1p_2\dots p_t 和 q1q2…qsq_1q_2\dots q_s ，我们首先说明 q1,q2,…,qsq_1,q_2,\dots,q_s 中至少有一个被 p1p_1 整除：

反证，由于 gcd(a,b)=1∧gcd(a,c)=1→gcd(a,bc)=1gcd(a,b)=1\land gcd(a,c)=1\to gcd(a,bc)=1 ，发现 p1∤q1,p1∤q2…p_1\nmid q_1,p_1\nmid q_2\dots 能导出 p1∤np_1\nmid n ，这就矛盾了

不妨设 p1∣q1p_1|q_1 ，因为它们都是质数所以 p1=q1p_1=q_1 ，根据归纳，剩下的部分的分解是唯一的，这就证完了

同余：a≡b(modm)a\equiv b \pmod m 表示 m∣a−bm|a-b

∃a\exists a 使得 ac≡1(modm)ac\equiv 1\pmod m 等价于 gcd⁡(c,m)=1\gcd(c,m)=1

我们称 Zm∗\Z_m^* 是 {n∈Zm∣gcd⁡(n,m)=1}\{n\in \Z_m|\gcd(n,m)=1\}

费马小定理

xp≡x(modp)x^p\equiv x \pmod p

对于任意正整数，则有 (x,n)=1→xφ(n)≡1(modn)(x,n)=1\to x^{\varphi(n)}\equiv 1\pmod n ，其中 φ(n)=∣Zn∗∣\varphi(n)=|\Z_n^*|

证明：考察 1,2,…,p−11,2,\dots,p-1 ，则 x,2x,…,(p−1)xx,2x,\dots,(p-1)x 模 pp 意义下和 1,2,…,p−11,2,\dots,p-1 是对应的，所以 (p−1)!xp−1≡(p−1)!(modp)(p-1)!x^{p-1}\equiv (p-1)!\pmod p

那么 xp−1≡1(modp)x^{p-1}\equiv 1\pmod p

然后再看任意正整数的情况，同样考察 A=∏i∈Zn∗iA=\prod\limits_{i\in \Z_n^*}i 。那么 ∏i∈Zn∗(ix)=A∗xφ(n)\prod\limits_{i\in Z_n^*}(ix)=A*x^{\varphi(n)} ，由于可以建立 ii 和 ixix 之间的双射，即 i=(ix−1)xi=(ix^{-1})x ，所以

A=A∗xφ(n)A=A*x^{\varphi(n)} ，所以 xφ(n)≡1(modn)x^{\varphi(n)}\equiv 1\pmod n

phi 的性质：m=∑d∣mφ(d)m=\sum\limits_{d|m}\varphi(d)

证明很简单：m=∑i=1m1=∑d∣m∑i[gcd(i,m)=d]=∑d∣mφ(md)=∑d∣mφ(d)m=\sum\limits_{i=1}^m 1=\sum\limits_{d|m}\sum\limits_{i}[gcd(i,m)=d]=\sum\limits_{d|m}\varphi(\frac{m}{d})=\sum\limits_{d|m}\varphi(d)

一种加密算法：取 N=pqN=pq ，其中 p,qp,q 是大质数。考虑信息 m∈ZN∗m\in \Z_N^* ，加密成 me mod Nm^e\bmod N 。秘钥是 dd 满足 ed mod φ(m)=1ed\bmod \varphi(m)=1 。解码： (me)d mod N=m(m^e)^d\bmod N=m 。

CRT

考虑 N=n1n2…ntN=n_1n_2\dots n_t ，其中 n1,n2,…,ntn_1,n_2,\dots,n_t 是互质的。

设 π:Zn→Zn1∗Zn2∗⋯∗Znt\pi:\Z_n\to \Z_{n_1}*\Z_{n_2}*\dots*\Z_{n_t}

满足 π(a)=(a mod n1,a mod n2,…a mod nt)\pi(a)=(a\bmod n_1,a\bmod n_2,\dots a\bmod n_t)

可以证明 π\pi 是双射，为什么呢？

其实就是要搞出来 π−1(a1,a2,…,at)\pi^{-1}(a_1,a_2,\dots,a_t) ，只需要设 bib_i 表示 Nni\frac{N}{n_i} 模 nin_i 的逆元，那么 ∑aibiNni\sum a_ib_i\frac{N}{n_i} 满足条件。

利用这个映射其实就可以证明 phi 为啥是积性函数了。